
Grade 4 Math
When we evaluate student work artifacts — the actual work students are asked to do in the classroom — one thing we count as an important strength is evidence of writing in math class.
Until relatively recently, the use of writing in math was almost non-existent. The Common Core helped usher in some use of writing in math, and we are seeing more of it, though its use is by no means universal or even consistent within or between schools in the same district. In general, we see it more in the elementary grades, and less and less in the secondary grades — which is unfortunate, because the increased complexity of secondary mathematics makes the use of writing to organize ideas and justify solutions even more valuable.
Why don’t we do more of this? When the first studies about math and writing began to be published in the 1990s and earlier, there was tremendous pushback from math teachers who felt that writing had no place in math: math was exclusively a world of numbers and formulas. Also, there was some predictable backlash on the grading front: would math teachers have to grade writing as though they were — gasp! — English teachers? Would English teachers be asked to grade math’s papers if they required writing? Sounds silly, I know, but I sat through these exact debates in the mid 90s when there was a big push for reading and writing across content areas. To say it has taken a while to catch on is a massive understatement.
Grade 4 Math – Gifted
Writing to Learn. Writing uses both hemispheres of the brain: one part generates ideas and the other organizes them and places them in a structure. Both halves work together to make meaning of new content by describing, ordering, evaluating, and justifying. We see this all the time in the marriage of writing and reading; it works exactly the same way in math. Asking kids to write about their mathematical understanding and justify their solutions requires them to use different parts of their brains than are usually employed in math processes — it helps them get to the conceptual level of the math, rather than staying at the level of execution. If math were only about execution, we’d all be math geniuses, memorizing formulas and firing them off with abandon. But problem-solution isn’t always a simple one-to-one correspondence. As math becomes more complex, there may be many ways to arrive at the same answer. If this is so, then being able to justify your solution is as important as arriving at it in the first place. There’s also a direct correlation between a student’s ability to explain math concepts and his/her ability to understand and apply them.

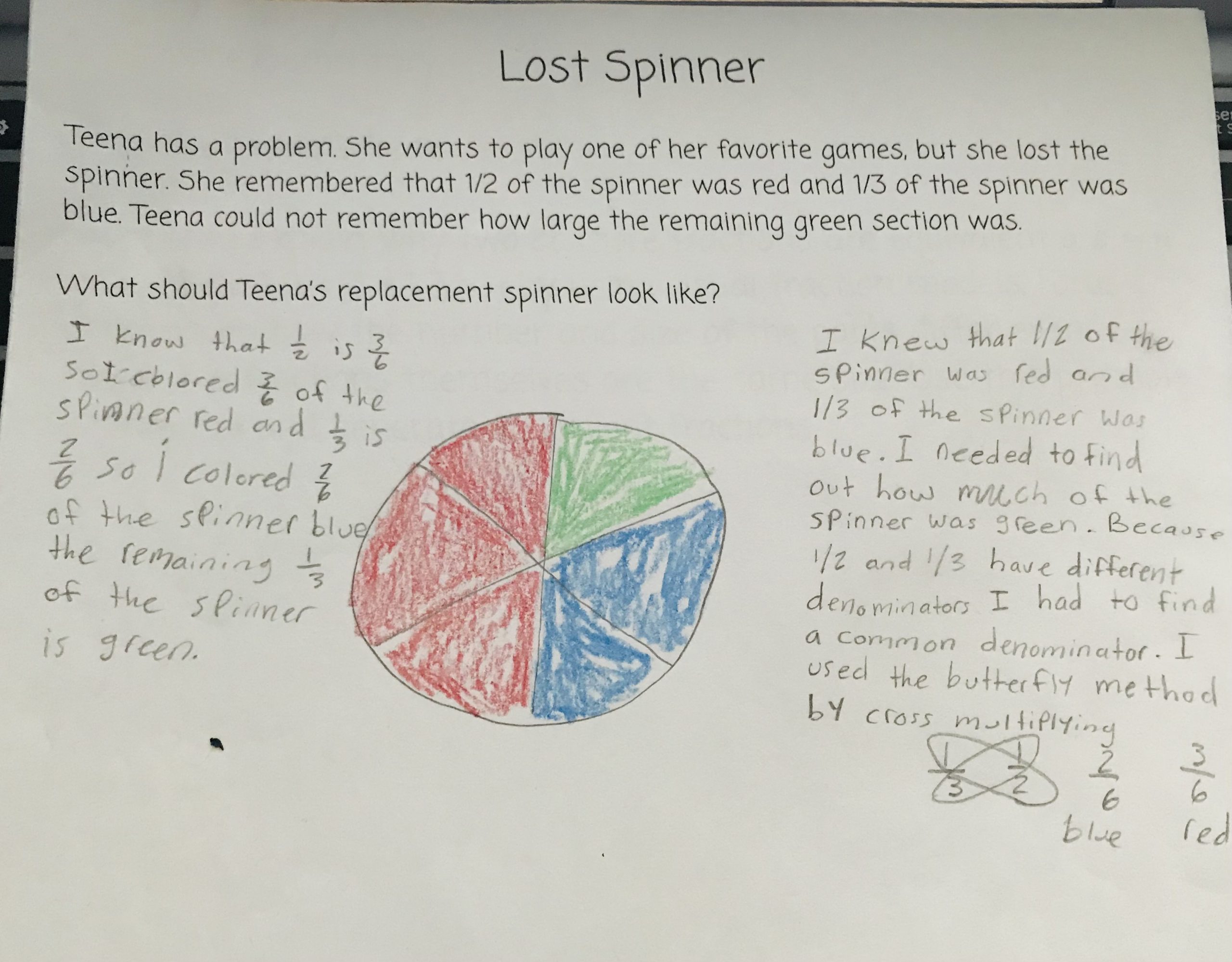
Grade 5 Math
Accessing Higher Order Thinking. Writing in math, especially writing to justify a solution, pushes the student’s thinking into higher levels of cognition. A lot of mathematical thinking hovers around Understanding and Applying. Asking a child to write about math and justify how s/he arrived at a solution or how s/he knows it’s correct pushes the thinking into Analyzing and Evaluating, while the act of writing about it and synthesizing the understanding into a paragraph qualifies as Creating. Using multiple means to represent understanding also helps consolidate learning from several directions at once, boosting retention. In two of the three examples here, the student has combined writing and pictures to clarify thinking and demonstrate how the solution works. Kids should begin doing this as early as possible. For pre-writers, dictation combined with drawing is a good way to help them begin to capture their understanding of math concepts on paper.
One thing that’s important here is that the writing in math is not graded as it would be in language arts. The goal is not grammatical correctness and precision punctuation, it’s consolidating learning by expressing thought processes and mathematical ideas. We’re looking for whether the student can justify or explain thinking and solutions, not whether he or she capitalizes appropriately. To a large extent, the child needs to be free of most of the constraints that might hinder expression and we absolutely don’t want to deduct points because they spelled something wrong (like remainder in the first example). They need opportunity to use mathematics vocabulary (like congruent, mean, quadrilateral, algorithm) in low-stakes environments.
Kids can get better at math….by writing.
